Aplicación del teorema de Bolzano (2º Bach)

El teorema de Bolzano nos asegura la existencia de al menos una raíz en un intervalo, siempre que se cumplen las condiciones. Pero en algunas ocasiones lo que queremos es demostrar que sólo tiene una solución.
Ejercicio. Demuestra que la ecuación  tiene una única solución real.

1. Existencia de soluciones. Aplico el teorema de Bolzano a la función que cumple las condiciones en el intervalo [0,1]: continuidad por ser polinómica y valores de signo contrario en los extremos de ese intervalo. Por lo tanto tenemos asegurada la existencia de al menos un c en dicho intervalo para el que f(c)=0.
2. La solución es única. Para demostrar que hay una única solución, utilizaremos el método de reducción al absurdo. Supongamos que hay al menos dos soluciones (a y b; a menor que b) que anulan la función f. Si eso es cierto, puedo aplicar el Teorema de Rolle a la función f, ya que verifica todas las condiciones: es continua en [a, b], es derivable en (a,b) y toma el mismo valor en los extremos del intervalo f(a)=0=f(b). Por lo tanto, aplicando dicho teorema, la derivada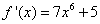se anula en algún punto perteneciente al intervalo (a,b). Pero vemos que es siempre positiva y no puede anularse (se produce una situación absurda). Por lo tanto,si suponer que hay más de un valor que anula la función f nos lleva a una contradicción, lo contrario será cierto: la solución es única.